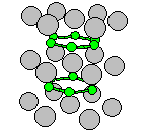
The hexagonal ω (C32) Structure
You can now
- This is the hexagonal ω phase. There is also a trigonal ω (C6) phase.
- For more details about the ω phase and materials
which form in the ω phase, see S.K. Sikka, Y.K. Vohra,
and R. Chidambaram, Progress in Materials Science
27, 245-310 (1982). Most ω phase
intermetallic alloys are disordered.
- One interesting thing about this structure is that the
B-B distance is smaller than the Al-B distance for every c/a
ratio. So if c/a is small enough the structure looks like a
set of inter-penetrating Boron triangular planes and Aluminum
chains. If c/a = 3-1/3 the Al-Al
distance along (001) is the same as the B-B distance in the
plane, and, for that matter, the B-B distance in the (001)
direction. This value (0.577) is close to the value
(3/8)1/2 (0.612) where the trigonal ω phase can transform to
the body-centered cubic (A2) lattice,
which probably explains the close connection between the
ω and bcc phases.
- The other interesting thing about this structure is that
the Boron atoms form graphite-like
sheets. For this reason, as of 7 Feb 2003, we've moved
this structure into the sp2 section of
the Carbon and Related Structures page.
- Prototype: AlB2
- Pearson Symbol: hP3
- Strukturbericht Designation: C32
- Space Group: P6/mmm (Cartesian and lattice coordinate listings
available)
- Number: 191
-
Reference: Villars and
Calvert, Pearson's Handbook, Vol. I, p. 656.
- Other systems with this structure: Ti (metastable),
MgB2, Be2Hf, CeHg2
-
Primitive Vectors:
| A1 |
= |
½ a X - ½
31/2 a
Y |
| A2 |
= |
½ a X + ½
31/2 a
Y |
| A3 |
= |
c
Z |
-
Basis Vectors:
| B1 |
= |
|
0 |
|
(Al) |
(1a) |
| B2 |
= |
1/3 A1 + 2/3
A2 + ½
A3 |
= |
½ aX +
12-½ a Y + ½
c Z |
(B) |
(2d) |
| B3 |
= |
2/3 A1 + 1/3
A2 + ½
A3 |
= |
½ a X -
12-½ a Y + ½
c Z |
(B) |
(2d) |
Go back to the
Carbon and Related Structures page.
Go back to Crystal
Lattice Structure page.

